DBSCAN

DBSCAN is short for Density-based spatial clustering of applications with noise. Given a set of points in some space, it groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions (whose nearest neighbors are too far away). DBSCAN is one of the most common, and most commonly cited, clustering algorithms.

Algorithm

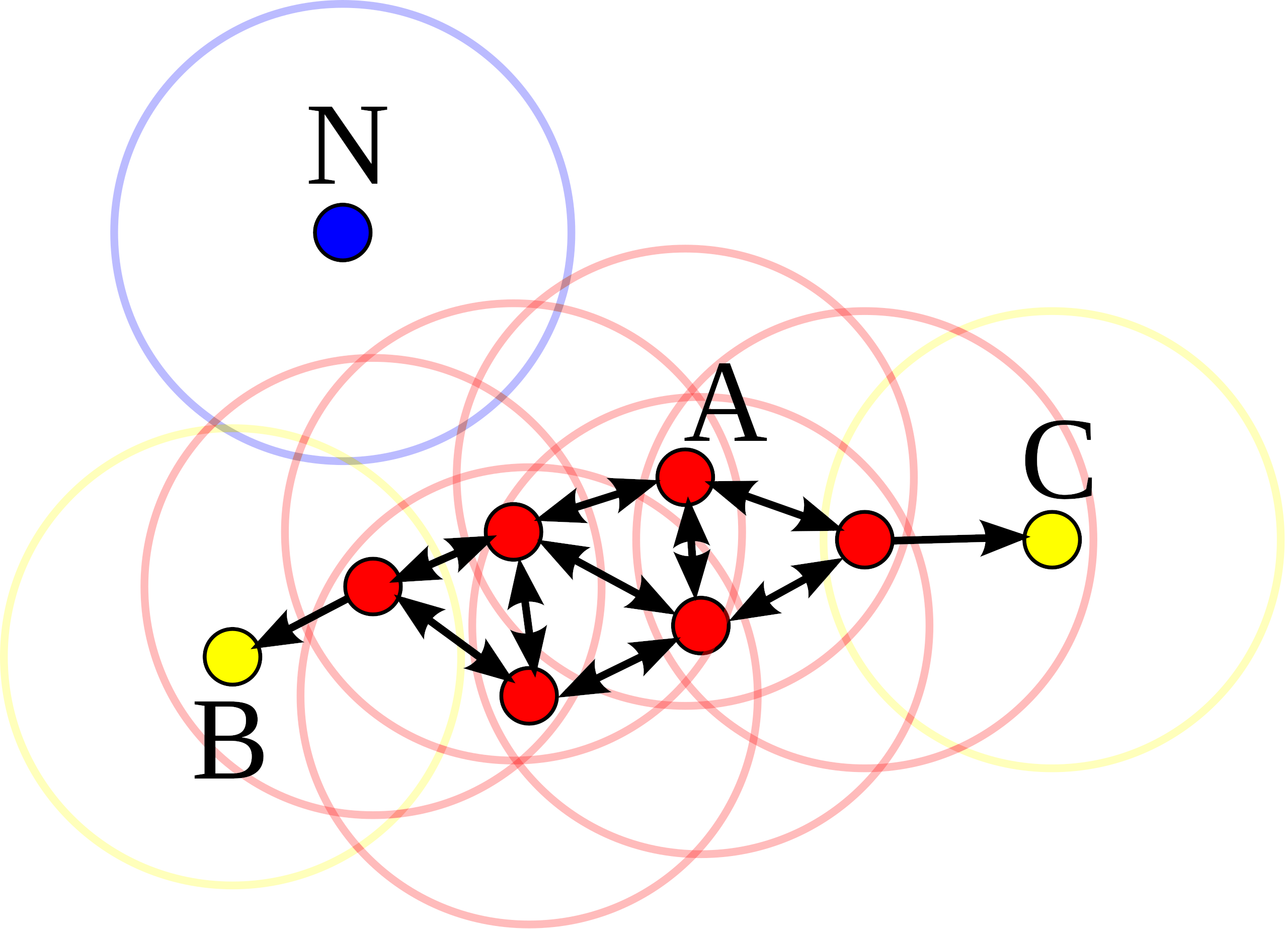
Consider a set of points in some space to be clustered. Let $\epsilon$ be a parameter specifying the radius of a neighborhood with respect to some point. For the purpose of DBSCAN clustering, the points are classified as core points, (directly-) reachable points and outliers, as follows:

• A point $p$ is a core point if at least minPts points are within distance $\epsilon$ of it (including $p$).
• A point $q$ is directly reachable from $p$ if point $q$ is within distance $\epsilon$ from core point $p$. Points are only said to be directly reachable from core points.
• A point $q$ is reachable from $p$ if there is a path $p_1,\dots ,p_n$ with $p_1=p$ and $p_n=q$, where each $p_{i+1}$ is directly reachable from $p_i$. Note that this implies that the initial point and all points on the path must be core points, with the possible exception of q.
• All points not reachable from any other point are outliers or noise points.

Now if $p$ is a core point, then it forms a cluster together with all points (core or non-core) that are reachable from it. Each cluster contains at least one core point; non-core points can be part of a cluster, but they form its "edge", since they cannot be used to reach more points.

Illustration

DBSCAN can find non-linearly separable clusters. The following dataset cannot be adequately clustered with [[K-Means]] or Gaussian Mixture EM clustering.

Pros

• DBSCAN does not require one to specify the number of clusters in the data a priori, as opposed to K-Means.
• DBSCAN can find arbitrarily-shaped clusters. It can even find a cluster completely surrounded by (but not connected to) a different cluster. Due to the MinPts parameter, the so-called single-link effect (different clusters being connected by a thin line of points) is reduced.
• DBSCAN has a notion of noise, and is robust to outliers.
• DBSCAN requires just two parameters and is mostly insensitive to the ordering of the points in the database.
• The parameters minPts and $\epsilon$ can be set by a domain expert, if the data is well understood.

Cons

• DBSCAN is not entirely deterministic: border points that are reachable from more than one cluster can be part of either cluster, depending on the order the data are processed. For most data sets and domains, this situation does not arise often and has little impact on the clustering result.

• The quality of DBSCAN depends on the choice of a distance. The most common distance metric used is Euclidean distance. Especially for high-dimensional data, this metric can be rendered almost useless due to the so-called "Curse of dimensionality", making it difficult to find an appropriate value for $\epsilon$. This effect, however, is also present in any other algorithm based on Euclidean distance.

• DBSCAN cannot cluster data sets well with large differences in densities, since the minPts-$\epsilon$ combination cannot then be chosen appropriately for all clusters.
• If the data and scale are not well understood, choosing a meaningful distance threshold $\epsilon$ can be difficult.