Support Vector Machine (SVM)

Support Vector Machine is a supervised learning algorithm that finds the optimal hyperplane to separate different classes in a dataset. It's effective for both linear and non-linear classification tasks, and it aims to maximize the margin between classes, providing robust generalization to new, unseen data.

Algorithm

Computing the soft-margin SVM classifier amounts to minimizing something of the form:

[\frac{1}{n} \sum_{i = 1}^{n} max (0, 1 - y_{i} (w^{T} x_{i} - b))] + λ ∥ w ∥^{2} .

Kernels

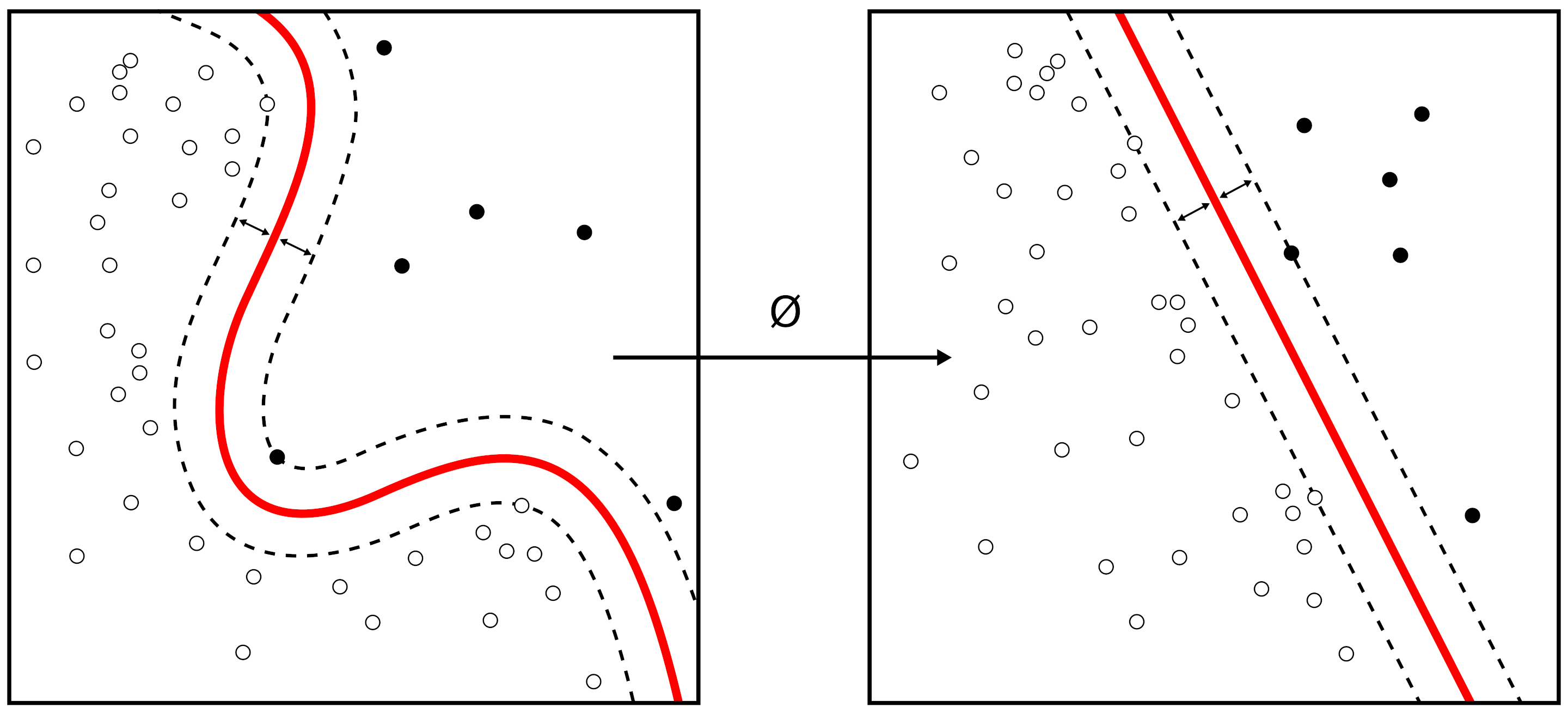
Every dot product is replaced by a non-linear kernel function. This allows the algorithm to fit the maximum-margin hyperplane in a transformed feature space. The transformation may be nonlinear and the transformed space high-dimensional; although the classifier is a hyperplane in the transformed feature space, it may be nonlinear in the original input space.

Some common kernels include

Polynomial: $k (u, v) = (u \cdot v)^{d}$ or $k (u, v) = (u \cdot v + r)^{d}$
Gaussian Radial Basis Function: $k (u, v) = \exp (- γ ∥ u - v ∥^{2})$ for some $γ > 0$ .
Sigmoid function: $k (u, v) = \tanh (κ u \cdot v + c)$ for some (not every) $κ > 0$ and $c < 0$ .

SVM_kernel.png | center | 550

Multiclass SVM (see Wikipedia)

Multiclass SVM aims to assign labels to instances by using support vector machines, where the labels are drawn from a finite set of several elements.

The dominant approach for doing so is to reduce the single problem into multiple binary classification problems. Common methods for such reduction include building binary classifiers that distinguish between one of the labels and the rest (one-versus-all) or between every pair of classes (one-versus-one). Classification of new instances for the one-versus-all case is done by a winner-takes-all strategy, in which the classifier with the highest-output function assigns the class (it is important that the output functions be calibrated to produce comparable scores). For the one-versus-one approach, classification is done by a max-wins voting strategy, in which every classifier assigns the instance to one of the two classes, then the vote for the assigned class is increased by one vote, and finally the class with the most votes determines the instance classification.

Pros

Effective in High-Dimensional Spaces: SVMs with kernels perform well in high-dimensional spaces, making them suitable for tasks with a large number of features.
Versatility with Kernels: the use of kernel functions allows SVMs to handle non-linear decision boundaries, making them versatile for a wide range of complex data distributions.
Effective in Non-Linearly Separable Data: SVMs with kernels are effective in handling non-linearly separable data by mapping it to a higher-dimensional space.
Robust to Overfitting: SVMs are less prone to overfitting, especially in high-dimensional spaces, due to the margin maximization objective.
Global Optimization Objective: SVMs aim to find a global optimum, leading to more stable and robust models compared to local optimization methods.
Memory Efficient: SVMs use a subset of training points (support vectors) for decision making, making them memory-efficient, especially when dealing with large datasets.
Works Well in Sparse Data: SVMs perform well in situations where the data is sparse, and the number of features is much greater than the number of samples.

Cons

Computational Complexity: Training SVMs with kernels can be computationally expensive, especially for large datasets. The time complexity often depends on the size of the dataset and the choice of the kernel.
Difficult to Interpret: SVM models, especially those with complex kernels, can be challenging to interpret and provide insights into the underlying relationships in the data.
Sensitivity to Noise: SVMs can be sensitive to noise in the training data, especially when using non-linear kernels. Outliers may have a significant impact on the decision boundary.
Parameter Sensitivity: The performance of SVMs with kernels is sensitive to the choice of hyperparameters, such as the regularization parameter and the kernel parameters. Tuning these parameters may require expertise.
Limited Scalability: SVMs with kernels may face challenges in scalability for very large datasets. Training time can become prohibitive as the dataset size increases.
Binary Classification: SVMs are originally designed for binary classification tasks. While there are extensions for multi-class problems, the fundamental algorithm is binary.
Memory Requirements: The memory requirements of SVMs can be high, particularly when using non-linear kernels and working with large datasets. This can limit their applicability in memory-constrained environments.