Linear Discriminant Analysis (LDA)
LDA is a statistical technique used for dimensionality reduction and classification. It aims to find a linear combination of features that best separates two or more classes in a dataset. LDA is commonly used in the context of supervised learning, where the goal is to maximize the distance between the means of different classes while minimizing the spread (variance) within each class.
The LDA decision rule depends on the data only through a linear combination of its elements, hence the world Linear in LDA.
Model
LDA assumes that the observations within each class are drawn from a multivariate Gaussian distribution with a class-specific mean variance and a common covariance matrix for all classes. See QDA for a model that relaxes this hypothesis.
Example
After performing PCA on the Iris dataset, we kept only the first two principal components (explaining 95% of the variance). Then, an LDA was performed. Below is a scatter plot of the first two principal components along with the decision boundaries of the LDA.
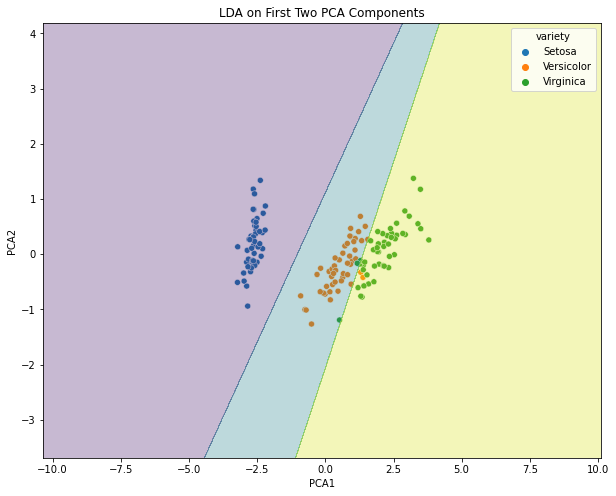
Pros
- Dimensionality Reduction: LDA projects data into a lower-dimensional space while preserving the class-discriminatory information. It's particularly useful when dealing with high-dimensional data.
- Maximizes Class Separation: LDA aims to maximize the distance between the means of different classes and minimize the spread (variance) within each class, making it effective for classification tasks.
- Works Well with Small Sample Sizes: LDA is relatively robust even when the number of training samples is small because the data is assumed to be Gaussian.
- Generative Model: LDA provides a probabilistic model for the distribution of the data, making it interpretable and allowing for the generation of new samples.
Cons of Linear Discriminant Analysis (LDA):
- Assumes Normality: LDA assumes that the features within each class follow a normal distribution. In cases where this assumption holds, LDA tends to perform well.
- Sensitive to Outliers: LDA is sensitive to outliers because it relies on the computation of means and covariances.
- Assumes Equal Covariances: LDA assumes that the covariance matrices of the different classes are equal. This assumption may not hold in real-world scenarios.
- Linear Decision Boundaries: LDA provides linear decision boundaries, which may limit its effectiveness in cases where the true decision boundaries are nonlinear.
- Not Robust to Irrelevant Features: LDA is not robust when irrelevant features are included in the dataset.