Quadratic Discriminant Analysis (QDA)
QDA is a classification and dimensionality reduction technique that extends LDA to accommodate non-linear decision boundaries. Unlike LDA, QDA does not assume equal covariance matrices for different classes, allowing for more flexibility in capturing complex relationships in the data.
Example
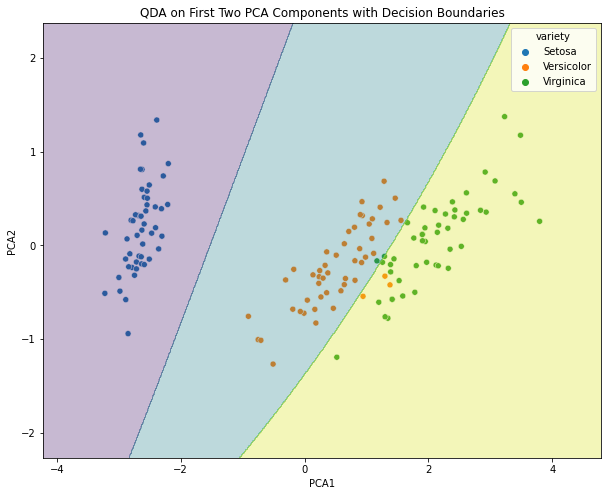
After performing LDA on the Iris dataset, we kept only the first two principal components (explaining 95% of the variance). Then, a QDA was performed. Below is a scatter plot of the first two principal components along with the decision boundaries of the QDA.
Pros
- Flexible Decision Boundaries: QDA allows for non-linear decision boundaries, making it more flexible than [[LDA]] when the covariance matrices of different classes are not assumed to be equal.
- Captures Class-Specific Covariance: QDA accommodates different covariance matrices for each class, which can be beneficial when the classes have distinct variances.
- Effective for Small Datasets: QDA is robust even with a limited number of training samples, as it does not involve the estimation of a shared covariance matrix.
- Non-Linear Dimensionality Reduction: QDA inherently provides non-linear dimensionality reduction, allowing for richer representations of the data.
Cons
- Computational Complexity: QDA involves estimating a covariance matrix for each class, making it computationally more demanding than LDA, especially with a large number of features.
- Sensitive to Outliers: QDA is sensitive to outliers because it estimates class-specific covariance matrices. Outliers can significantly impact the accuracy of covariance matrix estimation.
- Potential Overfitting: With a limited number of training samples, QDA may be prone to overfitting, especially when estimating individual covariance matrices for each class. Compared to LDA, it creates quadratic boundaries so the number of estimated parameters is far greater.
- Requires More Training Data: QDA may require a larger dataset compared to LDA to accurately estimate class-specific covariance matrices, especially in high-dimensional spaces.
- Assumption of Multivariate Normality: While QDA does not assume equal covariance matrices, it still assumes that the features within each class follow a multivariate normal distribution, which may not always hold in real-world data.