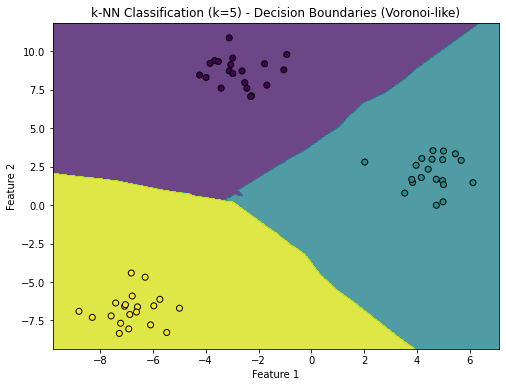
K-Nearest Neighbors

In statistics, the $k$-nearest neighbors algorithm ($k$-NN) is a non-parametric supervised learning method first developed by Evelyn Fix and Joseph Hodges in 1951, and later expanded by Thomas Cover. It is used for classification and regression. In both cases, the input consists of the k closest training examples in a data set. The output depends on whether $k$-NN is used for classification or regression:

• In $k$-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (k is a positive integer, typically small). If $k=1$, then the object is simply assigned to the class of that single nearest neighbor.
• In $k$-NN regression, the output is the property value for the object. This value is the average of the values of k nearest neighbors. If $k=1$, then the output is simply assigned to the value of that single nearest neighbor.

Illustration

If $k=1$ then the decision boundaries of the $k$-NN algorithm will be a Voronoi diagram. For $k>1$ it still kind of looks like one.